Is God a Mathematician?
Discovering the Mathematical Patterns That Shape Our World –Explore the Fascinating World of the Golden Ratio and Fibonacci Sequence, Where Mathematics Meets Nature’s Artistry
Prof. Aécio D’Silva, Ph.D
AquaUniversity
The Golden Ratio and Fibonacci Sequence – Mathematics is often viewed as a collection of numbers and equations confined to textbooks, but its true beauty lies in its prevalence in the world around us. Two mathematical concepts that exemplify this are the golden ratio and the Fibonacci sequence—patterns that appear in the most unexpected places, from the DNA, the bees, and the petals of a flower to the spirals of galaxies.
What Are the Golden Ratio and Fibonacci Sequence?
The golden ratio, denoted by the Greek letter phi (?), is approximately 1.618 and occurs when a line is divided into two parts so that the longer part divided by the shorter part is equal to the whole length divided by the longer part. The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, often starting with 0 and 1.
The Fibonacci Sequence:
The Fibonacci Sequence (SF) is infinite, where the following numbers are always the sum of the previous two numbers. That is, SF is a series of numbers where each number is the sum of the previous two, usually starting with 0 and 1.
That is:
(0 +1), = 1,
(1 plus 1) = 2,
(2 plus 1) = 3,
(3 plus 2) = 5,
(5 plus 3) = 8,
(8 plus 5) = 13,
(13 plus 8) = 21,
(21 plus 13) = 34,
(34 plus 21) = 55,
(55 plus 34) = 89,
(89 + 55) = 144 … and so on.
The Golden Ratio:
On the other hand, the golden ratio, also called the golden number, has a close relationship with the Fibonacci sequence. The golden ratio is an irrational algebraic real constant that represents, mathematically, the “perfection of nature.”
The golden ratio happens when a larger number of the Fibonacci sequence is divided by the smaller number immediately preceding it, we have a constant called the golden ratio, denoted by the Greek letter phi (?), which is approximately 1.618.
3 /2 = 1.5
5/3 = 1.666
8/5 = 1.6
13/8 = 1.625
21/13 = 1.615
34/21 = 1.619
55/21 = 1.618
89/55 = 1.618
144/89 = 1.618
233/144 = 1.618
377/233 = 1.618
……………………
The Golden Ratio also occurs when a line is divided into two parts so that the longer part is divided by the shorter part or equal to the entire length divided by the longer part.
The Golden Ratio in Nature
The golden ratio is not just a mathematical curiosity; it’s a natural phenomenon. It can be seen in the spiral arrangement of leaves, the pattern of seeds in a sunflower, and the branching of trees. This ratio provides a system of order and balance, contributing to the efficiency and beauty of natural forms in an intelligent design.
Who discovered the Fibonacci sequence?
Many sources claim that this sequence was first discovered or “invented” by Leonardo Fibonacci. The Italian mathematician, born around 1170 AD, was initially known as Leonardo of Pisa. In the 19th century, historians created the nickname Fibonacci (roughly meaning “son of the Bonacci clan”) to distinguish the mathematician from another famous Leonardo of Pisa.
To arrive at the sequence, Leonardo answered the following question: under ideal conditions, how many pairs of rabbits could be produced from a single pair of rabbits in a year? Surprisingly, the answer is 144 – and the formula used to arrive at this answer is none other than the Fibonacci sequence, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …. This hypothetical scenario assumes that rabbits always give birth to pairs, consisting of a male and a female.
Here’s how the scenario plays out: Initially, two newborn rabbits are placed in a fenced yard and left to breed. At the end of the first month, only the original pair remains, as rabbits cannot reproduce until they are at least one month old. At the end of the second month, the original pair gives birth, resulting in two pairs of rabbits. In the third month, the original pair produces another pair of newborns while the previous offspring reaches maturity, leaving three pairs of rabbits, two of which will reproduce and produce two more pairs the following month.
The total number of rabbits follows the Fibonacci sequence. After 12 months, there will be 144 pairs of rabbits. After two years, the number would rise to 46,368 pairs!
The Fibonacci Sequence in Nature
Similarly, the Fibonacci sequence manifests in various aspects of nature. The number of petals on a flower, the arrangement of a pinecone’s bracts, and the way a hawk spirals during flight all follow this sequence. It’s a testament to the sequence’s role in the growth patterns of living organisms.
How to Find the Golden Ratio
Finding the golden ratio involves a simple calculation. If you have a segment of length ‘a+b,’ where ‘a’ is the longer part and ‘b’ is the shorter part, the ratio ‘a/b’ should be approximately equal to 1.618, the golden ratio.
Spotting the Fibonacci Sequence
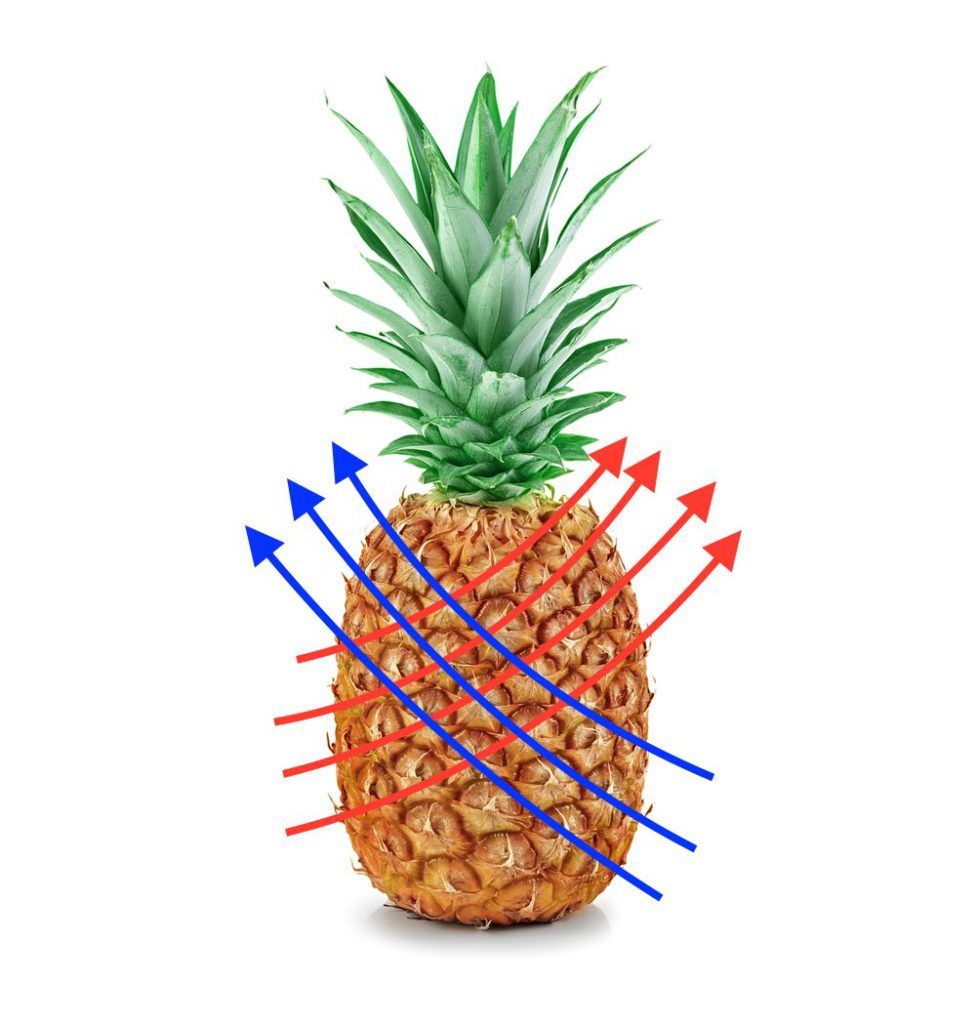
To spot the Fibonacci sequence, look for patterns that involve the sum of two preceding numbers. For example, the number of spirals on a pinecone or a pineapple typically follows the sequence.
The Golden Ratio in Daily Life
The golden ratio is more than a natural wonder; it’s a design principle. Architects and artists have used it to create aesthetically pleasing and harmonious works. It’s also used in product design, photography, and even in the stock market to predict price movements.
The Fibonacci Sequence in Our Routines
The Fibonacci sequence also has practical applications. It’s used in computer algorithms, financial models, and even in music composition. Recognizing this sequence can provide insights into various fields and phenomena.
How do scientists use the Fibonacci sequence to study plant growth?
Scientists use the Fibonacci sequence to study plant growth by examining the patterns in which leaves, seeds, and other plant parts are arranged. These patterns often follow the Fibonacci sequence, which can be seen in the arrangement of leaves around a stem or the seeds in a sunflower head. The sequence helps optimize the plant’s exposure to sunlight and nutrients, contributing to efficient growth.
The growth hormone auxin and the proteins that transport it play a crucial role in creating these patterns. Auxin influences where new seeds or leaves will form, and its distribution can lead to the Fibonacci sequence manifesting in the plant’s growth. For example, simulations have shown that the arrangement of sunflower seeds into spirals, which follow the Fibonacci sequence, results from the distribution of auxin within the plant’s meristem.
Additionally, some plants express the Fibonacci sequence in their growth points, the places where branches form or split. This pattern of growth allows for the most efficient packing of leaves or seeds, maximizing the plant’s ability to capture resources.
Understanding these patterns helps botanists and biologists decipher the underlying principles of plant growth and development, leading to insights into how plants adapt to their environment and how they can be bred for desirable traits.
Fibonacci sequence in Genetics
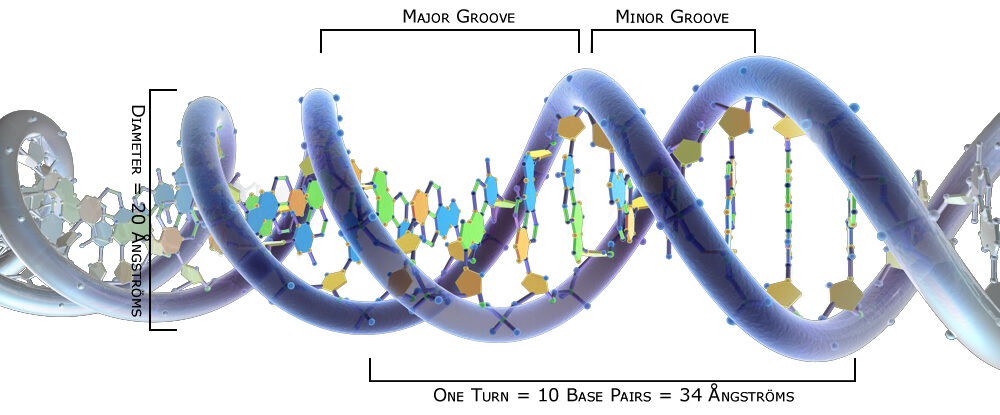
The Fibonacci sequence is present in many aspects of genetics, including the structure of the human body and the DNA molecule. The Fibonacci sequence is made up of numbers that are the sum of the previous two numbers. The sequence starts from 0 and 1, and the ratio of 34 angstroms to 21 angstroms in the DNA molecule’s double helix spiral is close to the Fibonacci ratio of 1.6190476 to 1.6180339.
The DNA’s double helix model relies on two assumptions. First, *Chargaff’s second parity rule should be valid, and second, the nucleotide frequencies should approach limit values when the number of bases is sufficiently large. Under these two hypotheses, it is possible to predict the human nucleotide frequencies with accuracy.
*(Erwin Chargaff, a professor of biochemistry at Columbia University Medical School, made significant contributions to the discovery of the double helix structure of DNA by uncovering two fundamental rules during his career.)
This result may be used as evidence of the Fibonacci string model that was proposed for the sequence growth of DNA repetitive sequences. It is noteworthy that the predicted values are solutions to an optimization problem, which is commonplace in many of nature’s phenomena.
The Fibonacci sequence is also used to predict human nucleotide frequencies. The model assumes that Chargaff’s second parity rule is valid and that nucleotide frequencies approach limit values when the number of bases is large enough.
Fibonacci sequence and DNA molecules. Even the microscopic realm is not immune to Fibonacci. The DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. These numbers, 34 and 21, are numbers in the Fibonacci series, and their ratio of 1.6190476 closely approximates Phi, 1.6180339.
In addition, the cochlea of the ear and the umbilical cord’s spiral are both Fibonacci spirals. The human face is said to have ratios equal to the Fibonacci ratio, including the relationship between the eyes, ears, mouth, and nose.
Here are some other applications of the Fibonacci sequence in science
The Fibonacci sequence has a wide range of applications in various scientific fields beyond its well-known presence in nature:
- Computer Science: It’s used in algorithms for efficient searching and sorting, such as the Fibonacci search technique, and in data structures like Fibonacci heaps (tree-based data structure) which optimize certain operations in computer programs.
- Cryptography: The sequence contributes to the development of cryptographic algorithms that ensure secure communication by creating complex codes that are difficult to decipher without a key.
- Quantum Computing: In quantum computing, the Fibonacci sequence can be used to model quantum systems and understand their behavior.
- Biology: Beyond plant growth, it helps model the population growth of species under ideal conditions and can be seen in the DNA (as seen above in the Fibonacci Sequence in Genetics) and in the structure and the branching patterns of some animals’ horns or shells.
- Artificial Intelligence: The sequence aids in creating algorithms that can learn from data in a more human-like manner, enhancing machine learning and artificial intelligence capabilities.
These applications demonstrate the Fibonacci sequence’s versatility and its profound impact on advancing scientific knowledge and technology.
How does quantum computing use the Fibonacci sequence?
Quantum computing utilizes the Fibonacci sequence in several intriguing ways. One of the most notable is the creation of a new phase of matter that behaves as if it has two distinct time dimensions. This was achieved by shooting a laser pulse sequence mimicking the Fibonacci sequence at a quantum computer. The sequence acted like a quasicrystal, which is ordered but not periodic, and this complex growth helped cancel out errors that typically occur on the edge of a quantum system. As a result, the quantum states were preserved much longer than usual, which is a significant advancement for the reliability of quantum computers.
Additionally, in topological quantum computing, systems of Fibonacci anyons* are used. These are particles that, as more are added to the system, the number of quantum states grows following the Fibonacci sequence. This property is beneficial for quantum computing as it allows for a more complex and potentially more powerful computing system.
*In the realm of physics, anyons represent a category of quasiparticles that have thus far been detected solely within two-dimensional systems. Unlike their counterparts in three-dimensional systems, which consist solely of fermions and bosons, anyons exhibit statistical characteristics that fall between those of fermions and bosons.
These applications of the Fibonacci sequence in quantum computing represent a step forward in tackling computational problems that are beyond the reach of conventional computers, leveraging the unique properties of quantum mechanics to store and process information in new and powerful ways.
How some fish and aquatic species express the Fibonacci sequence in their body and growth points
In the aquatic world, the Fibonacci sequence is expressed in various ways, reflecting the efficiency and optimization that this mathematical pattern offers in nature. Here are some examples of how fish and aquatic species exhibit the Fibonacci sequence:
- Phyllotaxis in Aquatic Plants: Some aquatic plants show the Fibonacci sequence in the arrangement of their leaves or petals, optimizing sunlight exposure and nutrient absorption.
- Shells and Spirals: Many shells, including those of snails and nautiluses, grow in a spiral pattern that can be mathematically described by the Fibonacci sequence. This allows for an even growth pattern that is structurally sound and can accommodate the organism’s increasing size without changing shape.
- Fish Scales: The pattern of scales on some fish may follow the Fibonacci sequence, which could be related to the way scales grow and provide protection without hindering flexibility.
- Teeth and Spines: The arrangement of teeth in some aquatic animals, or the spines on the back of a seahorse or sea urchin, can also exhibit patterns that align with the Fibonacci sequence, contributing to their functional effectiveness in defense or predation.
These patterns are not just aesthetically pleasing but also serve practical purposes, contributing to the survival and efficiency of aquatic species. The Fibonacci sequence in these biological structures is a testament to the pervasive influence of mathematics in the natural world.
To conclude, the golden ratio and the Fibonacci sequence are prime examples of how mathematics is deeply woven into the fabric of the universe. They remind us that there are God’s hands in the intelligent design of life, a pattern in the creation of nature. By understanding these concepts, we can appreciate God’s majesty and find inspiration in HIS intelligent design. As Galileo said: “God is indeed a mathematician”.
References:
- The intricate relationship between the golden ratio and Fibonacci sequence in nature https://www.treehugger.com/how-golden-ratio-manifests-nature-4869736https://www.mathnasium.com/blog/14-interesting-examples-of-the-golden-ratio-in-nature.
- Practical applications of the golden ratio in architecture and design https://www.invisionapp.com/inside-design/golden-ratio-designers/https://www.adobe.com/creativecloud/design/discover/golden-ratio.html.
- The Fibonacci sequence’s role in financial markets and computer algorithms. https://numberdyslexia.com/fibonacci-sequence-real-life-examples/https://sage-answer.com/how-is-fibonacci-used-in-everyday-life/.
- https://futurism.com/the-byte/fibonacci-quantum-computer.
- https://www.mathnasium.com/blog/14-interesting-examples-of-the-golden-ratio-in-nature
